STAT 385 Lab 5 Vectorization Help Document

Why Vectorization?

Avoid using for loops in R when possible.
Use vectorization whenever you can.

Kronecker Product

In mathematics, the Kronecker product, sometimes denoted by \(\bigotimes\), is an operation on two matrices of arbitrary size resulting a block matrix. It is a specialization of the tensor product (which is denoted by the same symbol) from vectors to matrices and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product.

You can find more information about Kronecker Product on Wikipedia https://en.wikipedia.org/wiki/Kronecker_product.

Mathemetical Definition of Kronecker Product

If \(\mathbf{A}\) is an \(m \times n\) matrix and \(\mathbf{B}\) is a \(p \times q\) matrix, then the Kronecker product \(\mathbf{A}\bigotimes \mathbf{B}\) is the \(pm \times qn\) block matrix:

\[\mathbf{A}\bigotimes \mathbf{B} = \begin{bmatrix} a_{11}\mathbf{B}\quad \cdots \quad a_{1n}\mathbf{B}\\ \vdots\quad \ddots\quad \vdots\\ a_{m1}\mathbf{B}\quad \cdots \quad a_{mn}\mathbf{B} \end{bmatrix},\]

more explicitly,

\[\mathbf{A}\bigotimes \mathbf{B} =\left[\begin{array}{cccccccccc} a_{11}b_{11}& a_{11}b_{12} & \cdots & a_{11}b_{1q}& \cdots& \cdots& a_{1n}b_{11}& a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ a_{11}b_{21}& a_{11}b_{22} & \cdots & a_{11}b_{2q}& \cdots& \cdots& a_{1n}b_{21}& a_{1n}b_{22} & \cdots & a_{1n}b_{2q} \\ \vdots& \vdots& \ddots& \vdots & & & \vdots& \vdots& \ddots& \vdots \\ a_{11}b_{p1}& a_{11}b_{p2} & \cdots & a_{11}b_{pq}& \cdots& \cdots& a_{1n}b_{p1}& a_{1n}b_{p2} & \cdots & a_{1n}b_{pq} \\ \vdots& \vdots& & \vdots & \ddots& & \vdots & \vdots& & \vdots \\ \vdots& \vdots& & \vdots & &\ddots & \vdots & \vdots& & \vdots \\ a_{m1}b_{11}& a_{m1}b_{12} & \cdots & a_{m1}b_{1q}& \cdots& \cdots& a_{mn}b_{11}& a_{mn}b_{12} & \cdots & a_{mn}b_{1q} \\ a_{m1}b_{21}& a_{m1}b_{22} & \cdots & a_{m1}b_{2q}& \cdots& \cdots& a_{mn}b_{21}& a_{mn}b_{22} & \cdots & a_{mn}b_{2q} \\ \vdots& \vdots& \ddots& \vdots & & & \vdots& \vdots& \ddots& \vdots \\ a_{m1}b_{p1}& a_{m1}b_{p2} & \cdots & a_{m1}b_{pq}& \cdots& \cdots& a_{mn}b_{p1}& a_{mn}b_{p2} & \cdots & a_{mn}b_{pq} \end{array}\right],\]

Kronecker Product Example

\[A = \begin{bmatrix} 1 \quad 3 \\ 2 \quad 4 \end{bmatrix}\]

\[B = \begin{bmatrix} 0 \quad 5 \\ 6 \quad 7 \end{bmatrix}\]

Then

\[\mathbf{A}\bigotimes \mathbf{B} = \left[\begin{array}{cccc} 1\times 0 & 1\times 5 & 3\times 0 & 3\times 5\\ 1\times 6 & 1\times 7 & 3\times 6 & 3\times 7\\ 2\times 0 & 2\times 5 & 4\times 0 & 4\times 5\\ 2\times 6 & 2\times 7 & 4\times 6 & 4\times 7 \end{array}\right] = \left[\begin{array}{cccc} 0 & 5 & 0 & 15\\ 6 & 7 & 18 & 21\\ 0 & 10 & 0 & 20\\ 12 & 14 & 24 & 28 \end{array}\right].\]

Calculate Kronecker Product in R

Let \(A\) and \(B\) be \(2 \times 2\) matrices as follows:

(A <- matrix(1:4, nrow = 2))
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4
(B <- matrix(c(0, 6, 5, 7), nrow = 2))
#>      [,1] [,2]
#> [1,]    0    5
#> [2,]    6    7

Method I: The `kronecker()` Function

A
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4
B
#>      [,1] [,2]
#> [1,]    0    5
#> [2,]    6    7
kronecker(A, B)
#>      [,1] [,2] [,3] [,4]
#> [1,]    0    5    0   15
#> [2,]    6    7   18   21
#> [3,]    0   10    0   20
#> [4,]   12   14   24   28

Method II: For Loop

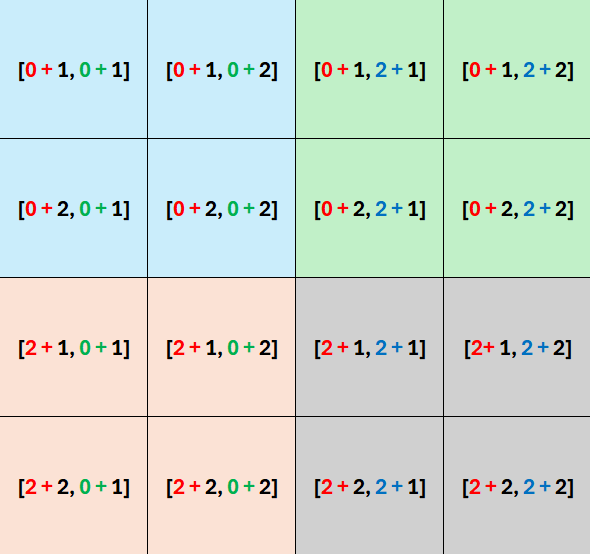
forloop_kronecker <- function(A, B){
  Res = matrix(NA, nrow = 2*2, ncol = 2*2)
  k = 0
  l = 0
  
  for (j in 1:2){
    k = 0
    for (i in 1:2){
      Res[(k+1):(k+2), (l+1):(l+2)] <- A[i, j] * B
      k = k + 2
    }
    l = l + 2
  }
  Res
}

forloop_kronecker(A, B)
#>      [,1] [,2] [,3] [,4]
#> [1,]    0    5    0   15
#> [2,]    6    7   18   21
#> [3,]    0   10    0   20
#> [4,]   12   14   24   28

Method III: Vectorization [Recommended]

Objective

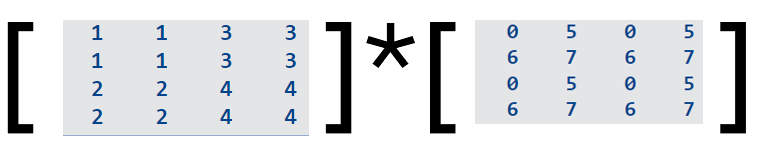
Deal with A

Recall

rep(1:2, each = 2)
#> [1] 1 1 2 2

A
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

A[rep(1:2, each = 2), rep(1:2, each = 2)]
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    1    3    3
#> [2,]    1    1    3    3
#> [3,]    2    2    4    4
#> [4,]    2    2    4    4

Deal with B